На груз действуют две силы: сила тяжести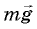 
и сила натяжения нити 
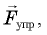направленная под углом ( к вертикали (рис. 15.4). Поскольку груз движется по окружности, равнодействующая этих сил обеспечивает центростремительное ускорение 
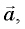направленное к центру окружности. Радиус окружности обозначим 
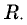Он связан с длиной нити и углом ее отклонения от вертикали соотношением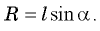 
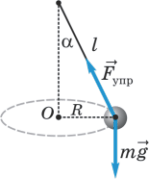 | Рис. 15.4. Силы, действующие на груз, подвешенный на нити, при движении по окружности. |
Согласно второму закону Ньютона,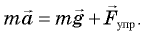 
Центростремительное ускорение связано со скоростью соотношением 
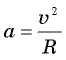(см. § 4. Криволинейное движение). Поскольку нас интересует период обращения 
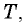выразим центростремительное ускорение через период, воспользовавшись соотношением 
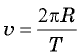(за время, равное одному периоду, груз совершает один полный оборот). Мы получим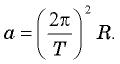 
Запишем уравнение второго закона Ньютона в проекциях на оси координат. Совместим начало координат с положением груза в данный момент, ось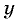 
направим вертикально вверх, а ось 
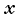— горизонтально вдоль радиуса к центру окружности. Из уравнения 
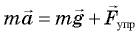мы получим систему двух уравнений:
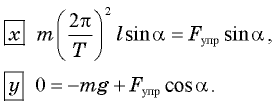
Из второго уравнения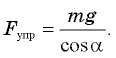 
Подставляя это выражение в первое уравнение системы, получаем 
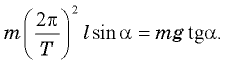Отсюда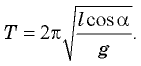 
Заметим, что если угол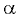 
достаточно мал, можно принять 
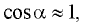и тогда получим 
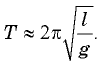В дальнейшем (см. § 20. Механические колебания) мы увидим, что таков же и период малых колебаний груза, подвешенного на нити.