Решение к задаче 3. Перемещение при неравномерном движении

Рассмотрим сначала равномерное прямолинейное движение. Если направить ось 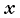вдоль прямой, по которой движется тело, то в проекциях на ось 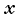получим: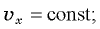 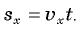Если изобразить график 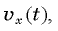то фигура, ограниченная этим графиком и осью 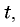будет прямоугольником, площадь которого численно равна 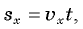то есть модулю проекции перемещения (рис. 5.3).

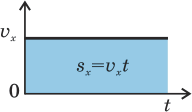Рис. 5.3. Фигура, ограниченная графиком проекции скорости при равномерном движении. Ее площадь численно равна модулю проекции перемещения.

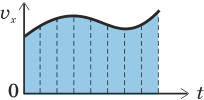
В случае неравномерного движения все время движения можно разбить на столь малые промежутки времени, что в течение каждого из них движение тела является практически равномерным (рис. 5.4), а затем сложить перемещения за все эти промежутки времени. В результате мы получим площадь фигуры, ограниченной графиком проекции скорости, что и требовалось доказать.

Рис. 5.4. Фигура, ограниченная графиком проекции скорости при неравномерном движении. Все время движения можно разбить на малые промежутки времени, в течение каждого из которых движение тела является практически равномерным.