Для нахождения мгновенного ускорения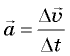 
надо найти, чему равно изменение скорости 
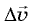за очень малый промежуток времени 
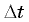(малый по сравнению с периодом обращения 
).
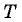Поскольку модуль скорости остается неизменным, скорость изменяется только по направлению, то есть изменение скорости за малый промежуток времени проявляется только в повороте вектора скорости на малый угол. Следовательно, векторы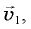 
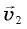и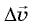 
образуют равнобедренный треугольник с очень малым углом при вершине (рис. 4.5). Но если угол при вершине равнобедренного треугольника стремится к нулю, то углы при его основании стремятся к прямым углам. А это означает, что когда промежуток времени 
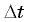неограниченно уменьшается, вектор изменения скорости 
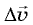будет направлен перпендикулярно вектору скорости, то есть по радиусу к центру окружности.
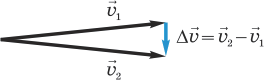 | Рис. 4.5. Изменение скорости при равномерном движении по окружности за малый промежуток времени. |
Следовательно,
По этой причине ускорение тела при движении по окружности называют центростремительным ускорением; модуль центростремительного ускорения обозначают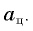 
Обратите внимание: направление ускорения (так же, как и направление скорости) при движении тела все время изменяется.
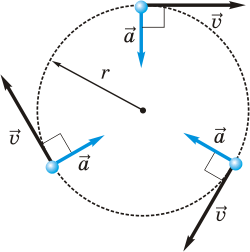 | Рис. 4.6. Направления скорости и ускорения тела при равномерном движении по окружности. |
Расчет показывает, что
Вывод этой формулы приведен в § 5. Примеры решения задач.