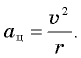Пусть за малый промежуток времени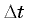 
тело переместилось из точки 1 в точку 2 (рис. 5.8). Обозначим 
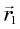и 
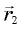векторы, проведенные из центра окружности в эти точки. Перемещение тела 
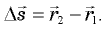Скорость тела в начальной точке обозначим 
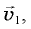а в конечной 
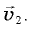Тогда вектор изменения скорости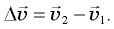 
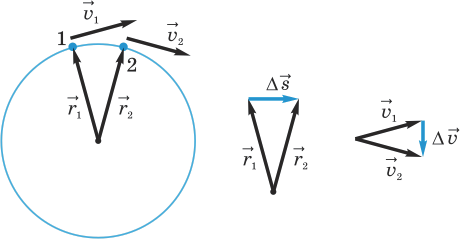Рис. 5.8. К выводу значения центростремительного ускорения.Заметим теперь, что треугольник, образованный векторам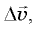и 
и 
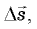
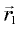подобен треугольнику, образованному векторами 
и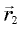 
(см. рис. 5.8), потому что оба треугольника равнобедренные, а углы при их вершинах равны (напомним, что скорость в каждой точке траектории перпендикулярна радиусу).
Модули векторов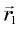 
и 
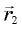равны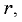 
а модули векторов 
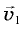и 
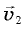равны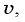 
поэтому из подобия указанных треугольников получаем 
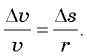Поскольку для малого промежутка времени 
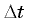можно принять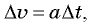 
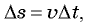где 
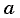и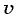 
— модули ускорения и скорости, получаем 
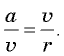Отсюда следует, что модуль центростремительного ускорения 