Чтобы ответить на поставленный вопрос, надо определить сначала, с каким ускорением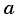 
будет двигаться брусок вдоль наклонной плоскости. Зная ускорение и пройденный путь 
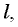можно будет найти скорость бруска в конце спуска, воспользовавшись уже выведенной нами формулой для равноускоренного движения 
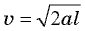(см. § 3. Ускорение. Прямолинейное равноускоренное движение).
На брусок, скользящий по наклонной плоскости, действуют три силы: сила тяжести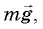 
сила нормальной реакции 
и сила трения скольжения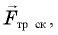 
направленная вдоль наклонной плоскости вверх.
Чтобы найти ускорение тела, надо воспользоваться вторым законом Ньютона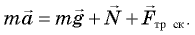 
Выбирая оси координат так же, как в рассмотренном выше примере, получаем:
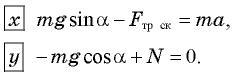
Кроме того, выполняется соотношение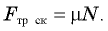 
Из второго уравнения системы следует, что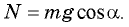 
Обратите внимание: для тела, находящегося на наклонной плоскости, сила нормальной реакции меньше силы тяжести. Отсюда следует, что 
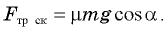Подставляя это соотношение в первое уравнение системы, находим, что ускорение бруска 
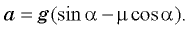Мы можем быть уверены в том, что это величина положительная, поскольку, согласно условию, брусок начал соскальзывать с наклонной плоскости — а это означает, в соответствии с предыдущим примером, что 
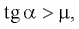то есть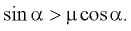 
Подставляя найденное выражение для ускорения в формулу для скорости в конце спуска, получаем 