Изучая падение тел, Галилей заметил, что скорость тел при падении увеличивается. Тогда он задался целью определить — как именно она увеличивается? Он предположил, что скорость тела при падении без начальной скорости увеличивается прямо пропорционально времени, то есть тело падает с постоянным ускорением. Но как проверить это предположение?
Галилей сначала значительно упростил задачу, доказав, что, если тело движется с постоянным ускорением без начальной скорости, то путь пропорционален квадрату времени движения. Однако измерить время падения с достаточной точностью Галилей не мог: в его распоряжении были только водяные часы (механических часов тогда еще не было).
Тогда Галилей догадался, что падение можно «замедлить», скатывая шары с наклонной плоскости. Уменьшая наклон плоскости, можно было добиться того, чтобы шар катился настолько медленно, что можно было производить измерения времени даже с помощью имеющихся у Галилея водяных часов.
Проведя тщательные измерения, Галилей установил, что путь, проходимый шаром, действительно прямо пропорционален квадрату времени движения, а это означало, что шар движется с постоянным ускорением. Далее Галилей заметил, что эта зависимость пути от времени остается справедливой при любом угле наклона плоскости. Отсюда Галилей сделал вывод, что и в предельном случае — когда плоскость становится вертикальной и шар уже не скатывается по ней, а просто падает, — он тоже движется с постоянным ускорением (рис. 3.3).
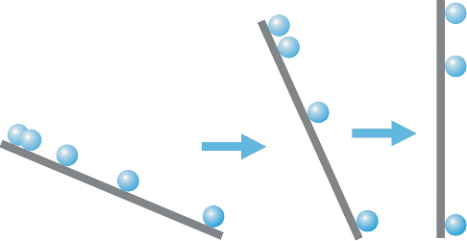Рис. 3.3. Переход от скатывания по плоскости к свободному падению.