Чтобы оценить размер атомного ядра, Резерфорд вычислил, на какое расстояние к положительно заряженному ядру должна приблизиться положительно заряженная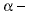 
частица, чтобы, оттолкнувшись согласно закону Кулона, изменить направление движения на противоположное. Полученный результат поразил физиков: оказалось, что атомное ядро в десятки тысяч раз меньше атома: размер ядра - около 
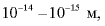а размер атома - примерно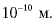 
Чтобы вы тоже смогли разделить удивление физиков того времени, приведем сравнение: ядро в центре атома подобно горошине посреди футбольного поля! И в этой «горошине» сосредоточена почти вся масса атома.
Это очень напоминало Солнечную систему: ведь и размеры Солнца очень малы по сравнению с размерами планетных орбит, а масса его примерно в тысячу раз больше суммарной массы всех планет, вместе взятых. Сходство атома с Солнечной системой усиливалось и сходством между законом Кулона и законом всемирного тяготения: в обоих случаях сила взаимодействия обратно пропорциональна квадрату расстояния.
Исходя из этого, Резерфорд предложил планетарную модель атома (см. рис. 26.4).
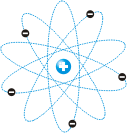 | Рис. 26.4. Планетарная модель атома: вокруг малого и массивного положительно заряженного ядра движутся по орбитам легкие электроны - подобно тому, как вокруг Солнца движутся планеты. |
Поскольку атом в целом электрически нейтрален, положительный заряд ядра равен по модулю суммарному заряду всех движущихся вокруг ядра электронов.