Как волновая теория объясняет законы отражения и преломления света?

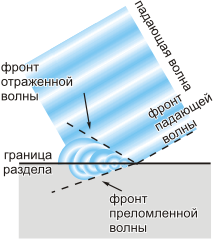
С помощью принципа Гюйгенса можно объяснить и преломление света на границе раздела двух прозрачных сред, если скорость света в этих средах различна.

Рассмотрим случай, когда плоская волна падает под углом на границу раздела двух сред.

Согласно принципу Гюйгенса, каждая точка этой границы сама становится источником сферических волн, причем эти волны распространяются в обе стороны от границы раздела (рис. 22.7).

Волны, идущие во вторую среду, формируют преломленную плоскую волну, а волны, возвращающиеся в первую среду, формируют отраженную плоскую волну.

Таким образом, принцип Гюйгенса убедительно объясняет, почему наряду с преломлением света всегда присутствует и отражение света.

Рис. 22.7. Объяснение отражения и преломления света согласно волновой теории. Каждая точка границы раздела двух сред является источником сферических волн, распространяющихся в обе стороны от границы раздела. На рисунке изображен случай, когда скорость света во второй среде (нижней на рисунке) меньше, чем в первой.

Используя несложные геометрические построения, можно доказать, что фронт отраженной волны образует такой же угол с плоскостью раздела двух сред, что и фронт падающей волны.

Отсюда следует уже знакомый вам закон отражения: угол отражения равен углу падения.

Рассмотрим теперь преломленную волну.

Предположим, что скорость света во второй среде меньше, чем в первой (на рис. 22.8 изображен как раз такой случай). Мы видим, что при этом фронт падающей волны составляет больший угол с поверхностью раздела сред, чем фронт преломленной волны. Поскольку фронт волны перпендикулярен направлению распространения света, углы между фронтом каждой волны и поверхностью раздела сред равны соответственно углам падения и преломления. Значит, в данном случае угол преломления меньше угла падения.

Расчеты показывают, что отношение синусов этих углов равно отношению скорости света в первой среде к скорости света во второй среде. А так как для двух данных сред это отношение постоянно, отсюда следует уже знакомый вам закон преломления: отношение синусов углов падения и преломления постоянно.

Итак, волновая теория света не только объясняет законы отражения и преломления света, но и раскрывает физический смысл показателя преломления: он равен отношению скорости света 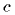 в вакууме к скорости света 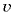в данной среде: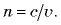

Таким образом, законы геометрической оптики являются следствиями волновой теории света, когда длина световой волны намного меньше размеров препятствий.