Решение многих задач, в которых используются векторные величины, значительно упрощается благодаря тому, что любую векторную величину можно задать с помощью нескольких чисел, называемых проекциями этой векторной величины на оси координат.
Если вектор направлен вдоль какой-либо одной из координатных осей, его проекция на эту ось равна модулю этого вектора, взятому со знаком «+», если вектор направлен в положительном направлении координатной оси, и со знаком «–», если вектор направлен в отрицательном направлении оси. Проекции же такого вектора на остальные координатные оси равны нулю.
Если направление вектора не совпадает с направлением какой-либо из координатных осей, его можно представить в виде суммы векторов, каждый из которых направлен вдоль одной из координатных осей. Такое представление называется разложением вектора на составляющие. В таком случае проекции вектора — это проекции его составляющих. На рис. 2.8 приведено разложение вектора на составляющие, одна из которых направлена вдоль оси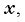 
а другая — вдоль оси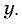 
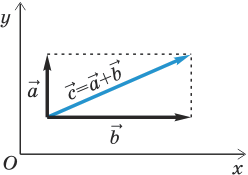Рис. 2.8. Разложение вектора на составляющие, направленные вдоль осей координат.Если, например, вектор скорости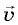 
лежит в плоскости 
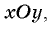он имеет две проекци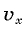и: 
и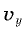 
(рис. 2.9).
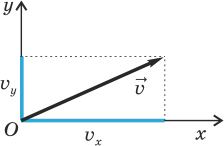Рис. 2.9. Вектор скорости и его проекции.В следующем пункте мы рассмотрим пример использования проекций скорости.