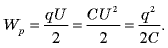Вывод формулы для энергии заряженного конденсатора

Раздвигая разноименно заряженные пластины конденсатора, мы совершаем положительную работу, так как пластины притягиваются друг к другу. При этом энергия конденсатора 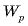Вывод формулы для энергии заряженного конденсатора 1 увеличивается на величину, равную совершенной нами работе 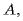Вывод формулы для энергии заряженного конденсатора 2 то есть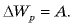 Вывод формулы для энергии заряженного конденсатора 3

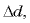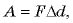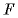Если увеличить расстояние между пластинами на Вывод формулы для энергии заряженного конденсатора 4 то совершенная работа Вывод формулы для энергии заряженного конденсатора 5 где Вывод формулы для энергии заряженного конденсатора 6- сила притяжения пластин, равная заряду 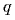Вывод формулы для энергии заряженного конденсатора 7 одной из пластин, умноженному на напряженность поля, создаваемого другой пластиной. Обе пластины дают равный вклад в напряженность поля 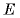Вывод формулы для энергии заряженного конденсатора 8 внутри конденсатора, поэтому напряженность поля, создаваемого одной пластиной, равна 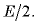Вывод формулы для энергии заряженного конденсатора 9 Таким образом, 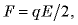Вывод формулы для энергии заряженного конденсатора 10 откуда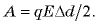 Вывод формулы для энергии заряженного конденсатора 11

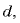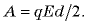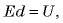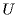Если начальное расстояние между пластинами равно нулю, а конечное равно Вывод формулы для энергии заряженного конденсатора 12 то совершенная при раздвигании пластин работа Вывод формулы для энергии заряженного конденсатора 13 Это и есть энергия заряженного конденсатора. Так как Вывод формулы для энергии заряженного конденсатора 14 где Вывод формулы для энергии заряженного конденсатора 15- разность потенциалов между обкладками конденсатора, получаем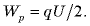 Вывод формулы для энергии заряженного конденсатора 16

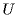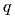Поскольку Вывод формулы для энергии заряженного конденсатора 17 и Вывод формулы для энергии заряженного конденсатора 18 связаны соотношением 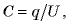Вывод формулы для энергии заряженного конденсатора 19 получаем три эквивалентные формулы для энергии заряженного конденсатора: Вывод формулы для энергии заряженного конденсатора 20



Электродинамика.