Согласно условию (тонкий подвижный поршень) давления и температуры газов одинаковы. Обозначим их 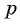 и
и 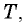 а массы газов (тоже равные) обозначим
а массы газов (тоже равные) обозначим 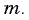 Объемы и молярные массы водорода и кислорода обозначим соответственно
Объемы и молярные массы водорода и кислорода обозначим соответственно 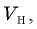
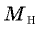 и
и 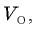
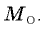 Запишем уравнения Менделеева—Клапейрона для этих газов:
Запишем уравнения Менделеева—Клапейрона для этих газов: 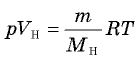 и
и 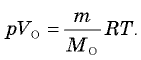 Деля почленно первое уравнение на второе, получаем
Деля почленно первое уравнение на второе, получаем 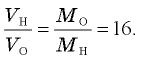 Следовательно, объем водорода в 16 раз больше объема кислорода, то есть при той же массе водород занимает 16/17 объема сосуда, а кислород — только 1/17. Обусловлено это «неравенство» тем, что при одинаковой массе газов число молекул водорода в 16 раз больше, чем число молекул кислорода. Полученный ответ — наглядная иллюстрация того, что многие свойства газов определяются не массой, а числом молекул!
Следовательно, объем водорода в 16 раз больше объема кислорода, то есть при той же массе водород занимает 16/17 объема сосуда, а кислород — только 1/17. Обусловлено это «неравенство» тем, что при одинаковой массе газов число молекул водорода в 16 раз больше, чем число молекул кислорода. Полученный ответ — наглядная иллюстрация того, что многие свойства газов определяются не массой, а числом молекул!
Решение к задаче 7. Уравнение состояния для переменной массы газа (уравнение Менделеева-Клапейрона)
Молекулярная физика и термодинамика. 2014
