Мы уже знаем, что число молекул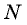 
связано с массой вещества 
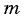и его молярной массой 
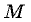соотношением 
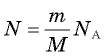(см. § 24. Количество вещества. Постоянная Авогадро). Подставляя это выражение в соотношение 
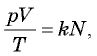получаем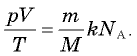 
Произведение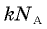 
обозначается 
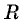и называется универсальной газовой постоянной. Измерения показали, что 
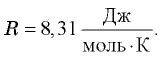Используя эту постоянную, получаем
уравнение Менделеева—Клапейрона: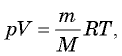 
где 
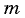— масса газа, 
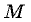— его молярная масса.
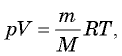где 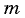— масса газа, 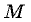— его молярная масса. Это уравнение было выведено русским ученым Менделеевым во второй половине 19-го века.